Benford’s Law Revised
After posting my previous article I started wondering why my transactional data contained a disproportional amount of twos. Something must be distorting the natural spread of first digits that Benford predicts. Later, while discussing this aberration with a friend, I finally figured it out.
It’s me. I distort the data. In fact, I distort the data every time I draw cash from an ATM.
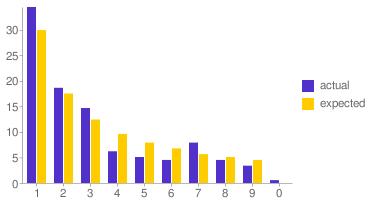
Like most people I have habits. One of them is that when I use an ATM I almost always withdraw twenty euros (I find cash a nuisance and prefer plastic, so I withdraw as little as I can manage). This, almost deterministic behavior, is the reason why there are a disproportionate amount of twos in the data. It seems my previous conclusion applies to the data in more ways than one.
Real-life data is obviously not random data, and when you think about it there are perfectly logical explanations for this result. If I remove ATM transactions from the original dataset the graph looks different. Still not exactly matching Benford’s prediction, but certainly a lot closer.
Update (april 2nd 2011): Code for this project is now available on Github.




