Benford’s Law
In a (not so) recent episode of Radio Lab (one of my favorite podcasts) I was introduced to Benford’s Law. I’d never heard of this phenomenon, which in hindsight is rather strange, because it’s effects are so profound. Let me explain.
Take a some numerical data from a real-life source, bank transaction amounts for instance, and tally the number of transactions whose amount starts with a one (i.e. whose first digit is a ‘1’ and not ‘2’ or ‘9’). What percentage of the transactions would you expect to match this criterion? What about the number of transactions whose amount starts with a three?
I’d never really though about this before. Implicitly I had always assumed that in large sets of data the distribution of first digits was equal amongst the numbers one through nine. This would result in the answer to the two questions above being “eleven percent” in both cases (zero is not considered, so there are nine possible first digits).
Benford’s Law predicts that I was wrong, and it turns out he is right.
The answers according to Benford’s Law are “probably about thirty percent” and “probably about twelve percent”. And using my own bank transaction amounts and some javascript gimmickry we can see that he is closer to the actual numbers than I was.
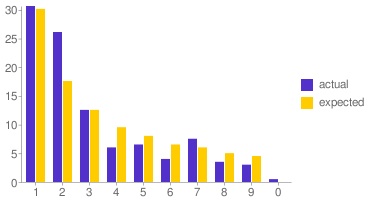
Real-life data is obviously not random data, and when you think about it there are perfectly logical explanations for this result. Still, for me, this is something I had to see in order to believe.
I encourage you to try it out yourself on your own data. I’m curious to know what you find.
Update (april 2nd 2011): Code for this project is now available on Github.




